Darstellung eines Gedanken-Experiments
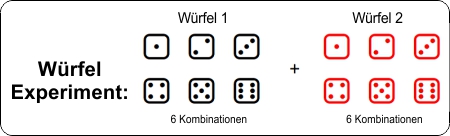
Würfel 1: Die möglichen Versuchsausgänge sind die sechs Augenzahlen: 1, 2, 3, 4, 5 und 6
+ Würfel 2: Die möglichen Versuchsausgänge sind die sechs Augenzahlen: 1, 2, 3, 4, 5 und 6
*Das Eintreten eines positiven Ereignisses beim zweiten Würfelwurf
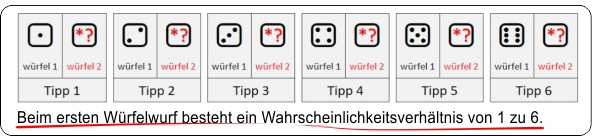
Für das Würfeln einer richtigen Zahl mit dem ersten Würfel gibt es einen Gewinn (Gewinnklasse 2, also 1+0). Wenn man eine weitere richtige Zahl mit dem zweiten Würfel würfelt, erhöht sich der Gewinn (Gewinnklasse 1, also 1+1). Wenn man nun die Gewinnwahrscheinlichkeiten berechnet, ergibt sich für das Würfeln einer richtigen Zahl mit dem ersten Würfel eine Gewinnwahrscheinlichkeit von 1:6, da es sechs mögliche Zahlen gibt, die gewürfelt werden können. Für das Würfeln von zwei richtigen Zahlen mit beiden Würfeln ergibt sich eine Gewinnwahrscheinlichkeit von 1:36, da es insgesamt 36 mögliche Kombinationen gibt (6 Möglichkeiten für den ersten Würfel mal 6 Möglichkeiten für den zweiten Würfel).
Wenn man eine richtige Zahl mit dem ersten Würfel würfelt, verringert sich die Anzahl der möglichen Kombinationen und somit auch die Gewinnwahrscheinlichkeit. Die Gewinnwahrscheinlichkeit beträgt dann nur noch 1:6 und nicht mehr 1:7,2, da die Kombinationen, bei denen die zweite Würfelzahl ins Spiel kommt, für dieses Spiel irrelevant sind.




